Paul Cohen

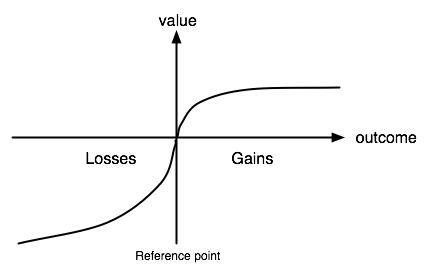
Prospect theory, outlined in 1979 by Kahneman & Tversky in what became one of the most cited papers in the social sciences [pdf], is the bedrock of modern behavioral economics. It’s often portrayed in the popular press as the instantiation of a phenomenon we can all intuit: the displeasure from losing $5 is worse than pleasure from gaining $5. This descriptive formulation belies the true power of the complex cognitive mechanics implied by prospect theory (e.g., the value function and the probability weighting function). Rather than describing the technical detail of these elements, we’ll instead focus on the three core features of risky choice derived from prospect theory, and talk about what they mean in plain English.

 

 

1. Value is relative to a reference point
What it means

Our perception of value is dependent on the relative change and not on the resulting (absolute) value.

 

Example

Person A starts out with $100K in assets and wins $900K in a lottery, and now has $1M to her name. Person B starts out with $2M and loses $1M, and now has $1M. Even though they have the same resulting net worth, person A will feel a lot better than person B.

 

Why it’s important

In Von Neumann-Morgenstern utility, which serves as the basis for expected utility theory (EUT), the end result of a gamble is the ultimate determinant of utility. Under EUT, whether the gamble is framed as a gain or a loss is irrelevant. In contrast, prospect theory holds that value is defined based on the relative change in wealth instead of the resulting levels of wealth.

 

 

2. Loss Aversion
What it means

The value function is steeper for losses than for gains.  As a result, we are much more sensitive to losses than gains of the same magnitude.

 

Example

If you lose $5, you’ll suffer a loss of utility that is greater than the gain in utility that you would feel from earning $5.

 

Why it’s important

Loss aversion causes risk aversion, which is when you prefer a gamble with a lower expected value at a higher probability to a gamble with a higher expected value at a lower probability. For example, most people prefer $20 with 100% certainty than a 50%/50% gamble of $50 or $0.

 

 

3. Diminishing Sensitivity for Losses and Gains
What it means

The value function is concave for gains, but convex for losses. As a result, the impact of an additional gain of $1 falls as the overall gain increases, and the impact of an additional loss of $1 falls as the overall loss increases. The degree of diminishment is equal for losses and gains.

 

Example

Replacing a $100 loss with a $110 loss has a greater impact than replacing a $1,000 loss with a $1,010 loss.  

 

Why it’s important

Diminishing sensitivity leads to risk aversion for gains (discussed above) and risk seeking for losses. For example, most people prefer a 50%/50% gamble between a loss of $0 and $1,000 than a certain loss of $500.